In this post, I write about the problem of sphere packing and augmented communication in the future of the bio- and technosphere.

Previously, I approached the topic of transitions in intelligence. I developed in some detail how minimal living systems becoming distributed can accelerate the evolution towards higher levels of intelligence, by bootstrapping the learning process within a network of computing nodes.
In the history of life, through the formation of the first social networks, living systems learned to accumulate information in a distributed way. Instead of having to sacrifice individuals from their population in exchange for information relevant to their survival, biological species became able to learn by simply exchanging ideas. A few millions of generations later, we see the start of the emergence of machine intelligence, which has arguably already managed to bring learning at levels never achieved before.
In this post, we will explore how connecting these intelligent machines in the future, through an increasingly interconnected and extremely high-bandwidth network, can bring about new paradigms of learning. I’ll try to flesh out the reasons for the power of this new learning, and why it may make for technology with even faster learning than current levels. The secret ingredient may be found in the advent of optimal communication protocols, developed by AIs for AIs.
By designing their own languages to communicate between each other to solve specific problems, AIs may undergo significant phase transitions in the way they represent information. These representations would then effectively become projections of reality that can propel them to unveiled levels of problem solving.
The theories that I rely on in the following are based on computational learning, complexity, formal linguistics, mathematical sphere-packing and coding theories.
About AI
As Max Tegmark notes it in his recent book, life is now entering its third age. Through research advances in artificial intelligence (AI), life becomes capable of modifying not only its own software via learning and culture, but it can now also edit its own hardware. As an ALifer (Artificial Life researcher), this hits particularly close to home.

Hyperconnected society
Combined with the advent of the Internet, half a century ago, human society has undergone a crucial transition in connectivity, which I’d argue has the power to drastically alter the structure of communication, in very unpredictable ways.

Communication
What is the nature of communication? How does signaling vary across existing and past species in biology? What will it be like to speak to each other in the future, with the advances of AI technology? How will future forms of intelligence communicate, whether they are natural, artificial, or a mixture of both? How distant will their communication system be from human language?
There is a large amount of literature on the evolution of communication, from simple signaling systems to complex, fully-fledged languages (Christiansen 2003; Cangelosi 2012). However, while most research in biology focuses on the natural evolution of communication systems, computer science has for a long time been engineering and optimizing protocols for specific tasks, for example for applications in robotics and computer networks (Corne 2000). Underneath and across all these systems, lives a fundamental theory of communication which studies its rich structure and fascinating properties, as pioneered by Shannon (1948). Later, Chomsky (2002) and Minsky (1974) would contribute with formal theories about the structure, rules, and dynamics of language and the mind. In the following, I propose we look at communication from the perspective of sphere packing in high-dimensional spaces.
Multichannel Communication
With communication becoming largely digital, humankind has constructed itself a new niche, which has the power to change its cognitive capacity, like never before. The fact that communication is becoming free. Of course, like for most attempts of futuristic predictions, the impact of multiple channels on the future of communication being highly multichannel. One may wonder the effects of a highly connected society.
This is a question we can ask using tools from artificial life and coding theory. Here, I propose a combination of evolutionary computation with insights from coding theory, in order to show the effect of broadening channels on communication systems.
Sphere Packing Theory
Sphere packing in Euclidian spaces has a direct interpretation in error-correcting codes with continuous communication channels (Balakrishnan 1961). Since real-world communication channels can be modeled using high-dimensional vector spaces, high-dimensional sphere-packing is very relevant to modern communication.
The dimensionality of a code, i.e. the number of dimensions in which it encodes information, corresponds to the number of measurements describing codewords. Radio signals, for example, use two dimensions: amplitude and frequency.
The general idea, when one desires to arrange communications so as to remove the effects of noise, is to build a vocabulary of codewords to send, where
is an error-correcting code.
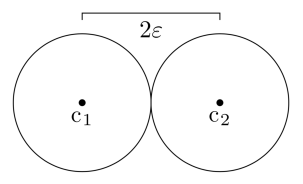
If two distinct codewords satisfy
, where
is the level of noise, the received codeword could be ambiguous, as the noise level may bring it beyond its sphere of correction.
The challenge is to pack as many -balls as possible into a larger ball of radius
, with R the maximal power radius allowed to achieve with given amounts of energy to send signals over the channel, which amounts to the sphere packing problem (Cohn 2016). With high-dimensional spaces, the usual packing models seem to break down, and apart from cases exploiting specific properties of symmetry (Adami 1995), largely unsolved.
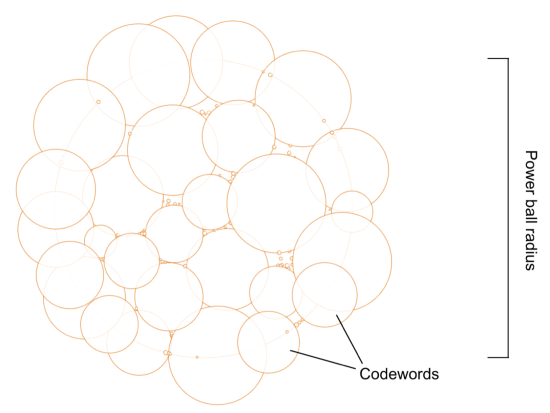
An Evolutionary Simulation
To get a feel of a problem of some complexity, my sense is usually to start coding and talk later. I therefore coded up a simulation, an evolutionary toy model in which to explore the influence of increasingly high dimensional channels of communication on structures of languages used by a network of agents to communicate over them.
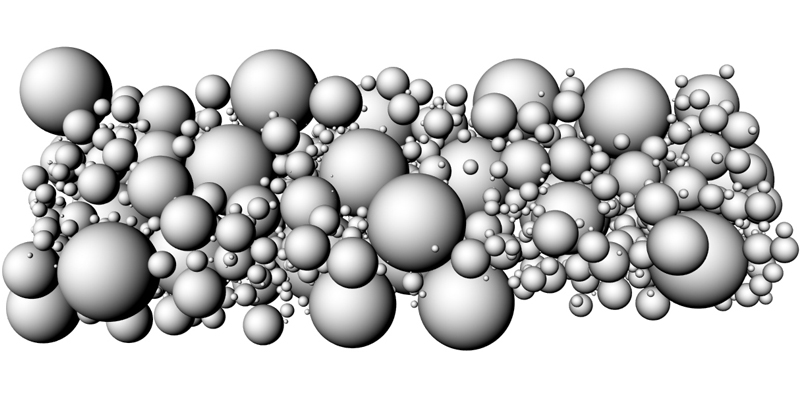
In the simulation, agents need to optimize a fitness function equal to the sum of successfully transmitted messages of large importance to other agents, over a variety of channels over a given range of dimensions, organized in randomly generated small-world networks, over their lifetime. Each agent’s genotype encodes a specific set of points distributed over a multidimensional space of a fixed range of sizes between m and n. The simulation then runs over many generations of agents adapting their communication protocol through mutation and selection by the genetic algorithm. I varied the values of m and n between 1 and 100 dimensions.
The simulation yields a sphere packing as illustrated below, which shows a packing for a two-dimensional channel, after 500 generations. Note that visualizing gets much trickier after three dimensions. You can squeeze a fourth and a fifth dimension in with a clever use of colors and types of strokes, but they usually don’t help the intuition. I personally find cuts and projections much more helpful to think about these problems, but that can be the topic for a future post. The point is, one notices that the more the simulation progresses, the more it improves its chances to asymptotically get to an optimally dense packing.

VS. Numerical Optimization
I compared these results to a collision-driven packing generation algorithm, using a variant on both the Lubachevsky–Stillinger algorithm (Lubachevsky 1990) and the Torquato-Jiao algorithm (Torquato 2009), so that it would be easily generalizable to n dimensions. This numerical procedure simulates a physical process of rearranging and compressing an assembly of hard hyperspheres, in order to find their densest spatial arrangement within given constraints, by progressively growing the particles’ size and adapting parameters such as spring constant and friction. The comparison showed that the solution reached by evolutionary simulations was consistently suboptimal, for the whole range of experiments.
Simulation results indicate that for higher dimensionality, the density ratio undergoes several transitions, in a very irregular fashion, which we can visualize in the form of difference in derivative of densities with respect to number of dimensions.
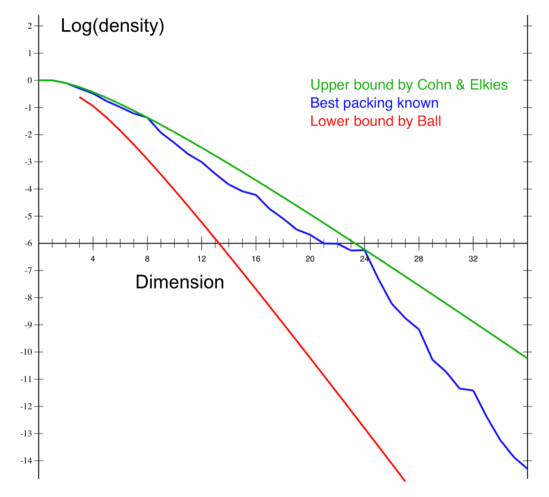
This may actually be expected, based on known solutions (analytical and numerical estimates) from sphere packing theory for dimensions up to 36 (Cohn 2016, see Figure above). Nevertheless, the existence of optimal packing solutions does not preclude from inherent difficulty to reach them within the framing of a particular dynamical system, and evolutionary computation depends strongly on simplicity and evolvability of encodings in the genotypic space.
So what?
An interesting property observed across these preliminary results is the frequency of jammed codes, that is, codes for which the balls are locked into place. This seems to be especially the case with spheres of different dimensions, although this is a hypothesis deserving further investigation. Further analysis will be required to fully interpret this result, and assess whether higher dimensions end up in crystalline distributions or fluid arrangements.
One important consideration is the fact that the evolutionary simulation may prefer dynamical encoding of solutions, but that’s also something to detail in its own post.

Beyond AI
This post was initially written thinking with in mind the ALIFE 2018 conference in Tokyo this year, which I was co-organizing.

The present post ois related to a piece of work worked on earlier this year, and on which I actually presented early results at the conference. The theme of ALIFE 2018 inspired research that goes “beyond AI”, using artificial life culture to ask the futuristic questions about the next transition in the evolution of human society.

The preliminary results suggest that future intelligent lifeforms, natural or artificial, from their interaction over largely broadband-channel networks, may invent novel linguistic structures in high-dimensional spaces. With new ways to communicate, future life may achieve unanticipated cognitive jumps in problem solving.
References
[1] Eörs Szathmáry and John Maynard Smith. The major evolutionary transitions. Nature, 374(6519):227–232, 1995.
[2] Max Tegmark. Life 3.0. Being Human in the Age of Artificial Intelligence. NY: Allen Lane, 2017.
[3] Claude E Shannon. A mathematical theory of communication (parts i and ii). Bell System Tech. J., 27:379–423, 1948.
[4] Nihat Ay. Information geometry on complexity and stochastic interaction. Entropy, 17(4):2432–2458, 2015.
[5] AV Balakrishnan. A contribution to the sphere-packing problem of communication theory. Journal of Mathematical Analysis and Applications, 3(3):485–506, 1961.
[6] Henry Cohn. Packing, coding, and ground states. arXiv preprint arXiv:1603.05202, 2016.
[7] Boris D Lubachevsky and Frank H Stillinger. Geometric properties of random disk packings. Journal of statistical Physics, 60(5-6):561–583, 1990.
[8] Salvatore Torquato and Yang Jiao. Dense packings of the platonic and archimedean solids. Nature, 460(7257):876, 2009.
[9] Günter P Wagner and Lee Altenberg. Perspective: complex adaptations and the evolution of evolvability. Evolution, 50(3):967–976, 1996.
